В каждой профессии есть свой набор любимых вопросов. Для исследователей рынка этот список возглавляет, безусловно, вопрос о размере выборки. Обычно его формулируют так:
- Мы хотели бы заказать исследование по посетителям московских торговых центров. Какая нам нужна выборка?
- Наша целевая аудитория – примерно 300 000 человек. Сколько людей нам нужно опросить, чтобы было репрезентативно? А если целевая аудитория будет 3 млн?
-
Нам нужно оценить потенциал продаж квартир в Санкт-Петербурге жителям северных городов России. Какую сделать выборку?
Размер выборки действительно важен, потому что определяет стоимость будущего исследования, не говоря уже о качестве итоговых результатов и выводов. В этой статье мы расскажем о том, как рассчитать оптимальный размер выборки массового опроса. Наш материал будет полезен всем, кто так или иначе сталкивается с необходимостью проведения маркетинговых исследований своими силами или заказывает их у специализированного агентства.
Главное заблуждение о размере выборки
Многие уверены, что чем больше размер целевой группы, тем больше должен быть размер выборки. Поэтому, якобы, чтобы узнать мнение жителей маленького города, достаточно опросить человек 200-300, ну а для выяснения мнения по России в целом и 5000 будет мало.
Между тем, этот стереотип не имеет ничего общего с реальностью. Размер выборки не зависит от численности целевой группы (на языке статистики она называется «генеральной совокупностью») и определяется двумя совершенно другими факторами. Единственное исключение из этого правила – случаи, когда генеральная совокупность очень маленькая, например, 1-2 тысячи человек, но такие ситуации в реальной практике маркетинговых исследований встречаются редко.
Два фактора, от которых зависит размер выборки
Размер выборки массового опроса зависит от двух факторов:
- Точности данных, которые нужно получить на выходе – это та самая «статистическая погрешность». Для выборки в 100 респондентов она будет в пределах плюс-минус 10%, а для выборки в 1000 респондентов – в пределах плюс-минус 3,1%. Более подробно об этом – ниже.
- Количества и размера подгрупп, на которые нужно разбивать выборку при анализе. Например, если проводится электоральное исследование, то в основном нас будет интересовать ядро активных избирателей. Как правило, доля «ядра» редко превышает 20-25% от всего населения. Поэтому размер выборки нужно рассчитывать так, чтобы одна четверть от ее общего объема позволяла проводить полноценный статистический анализ.
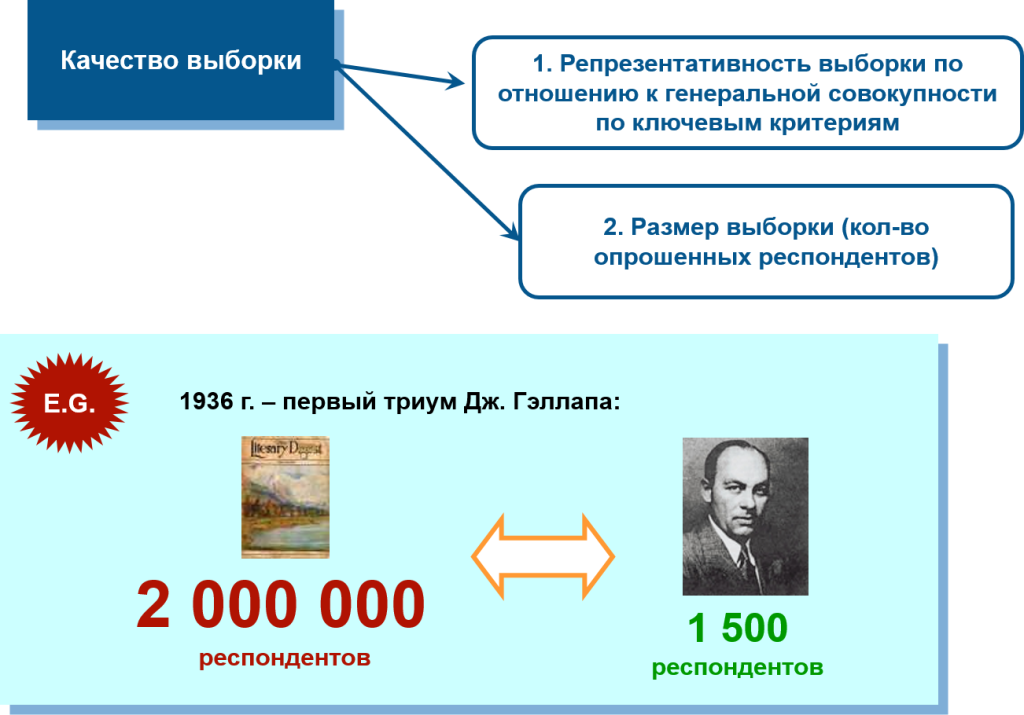
Вопреки расхожему мнению, качество выборки определяется не ее размером, а репрезентативностью. Репрезентативность – это соответствие между выборкой и генеральной совокупности по ключевым параметрам. Чаще всего, в качестве таких «реперных точек» используют легко измеряемые социально-демографические показатели: пол, возраст, образование, род занятий и место жительства.
 Две разновидности ошибки выборки
Две разновидности ошибки выборки
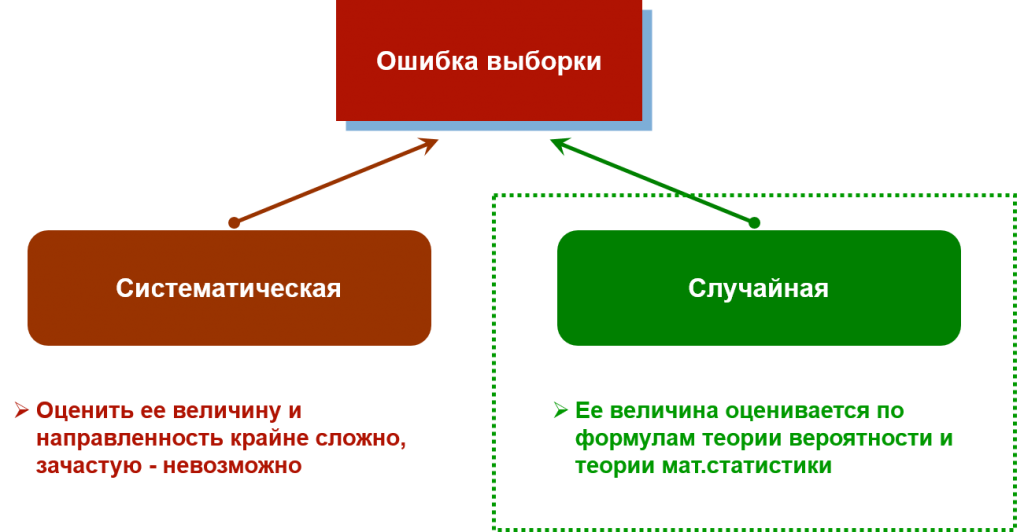
Любое выборочное наблюдение (то есть когда мы опрашиваем не всех подряд, а делаем случайный отбор из генеральной совокупности) сопряжено с погрешностью данных. Эту погрешность обычно называют «ошибкой выборки». Она может быть двух видов:
- Систематическая – связана с ошибками проектирования выборки. Оценить ее размер, направление и степень смещения очень сложно, чаще всего – невозможно. Например, если вопросы респондентам будут задавать представители маргинальных социальных слоев, это повлияет на готовность участвовать в исследовании со стороны представителей более обеспеченных групп населения. В итоге это приведет к крайне трудно оцениваемой систематической ошибке и искажению данных.
- Случайная – связана с действием законов статистики. Ее размер легко рассчитывается по формулам математической статистики и теории вероятности. Они позволяют делать обоснованные выводы о доверительном интервале признака. Например, если статистическая погрешность составляет плюс-минус 10%, а полученное значение показателя оказалось равно 25%, то доверительный интервал равен от 15% до 35%.
Задача исследователя – собрать данные так, чтобы минимизировать систематическую ошибку выборки. Тогда можно будет свести статпогрешность лишь к случайной ошибке, которую можно рассчитать по формулам.
Как рассчитать размер случайной ошибки выборки
Случайная ошибка выборки зависит не только от объема выборки, но и от дисперсии, то есть степени однородности данных. Чем однороднее данные (т.е. чем меньше разброс полученных значений, или дисперсия), тем меньше ошибка выборки.
Существует формула расчета случайной ошибки выборки, однако для удобства рекомендуем пользоваться онлайн-калькуляторами, например,
вот этим. Он позволяет легко провести два вида расчета:
- рассчитать величину статистической погрешности на основе размера выборки и предполагаемой дисперсии;
- определить размер выборки, требуемый для получения оценки нужной степени точности.
Вот так выглядит его рабочее окно:

В качестве параметра доверительной надежности (одно из полей в калькуляторе) обычно используется значение в 95%. Это означает, что в 95% случаев распределение признака в генеральной совокупности попадет в рассчитанный доверительный интервал (т.е. само значение признака в выборке плюс-минус размер статистической погрешности). Реже используется значение надежности в 97% или 99% – оно, соответственно, означает, что подобное попадание произойдет в 97% или 99% случаев. В данном случае надежность выборки повышается, но увеличивается размер выборки.
Самое сложное при определении размера выборки – поиск компромисса между требуемой точностью и стоимостью сбора данных. Этот процесс усложняется тем, что увеличение размера выборки в четыре раза приводит к увеличению точности лишь в два раза (соответствует квадратному корню от величины прироста выборки).
Кейс: определение размера выборки для оценки потенциала рынка продаж столичной недвижимости покупателям из регионов
В ноябре-декабре 2016 года мы провели исследование спроса на квартиры в новостройках Москвы и Санкт-Петербурга со стороны жителей разных городов России. Исследование включало в себя три метода сбора данных: массовый репрезентативный опрос населения в возрасте от 20 до 60 лет (проводился с использованием технологии CATI), а также серию экспертных интервью с риэлторами и глубинных интервью с потенциальными покупателями квартир.
Исследование охватывало 33 города, отличающихся повышенным спросом на петербургскую и московскую недвижимость. Плановая выборка исследования, рассчитанная по формулам, составила 21 500 респондентов. Этот объем значительно больше «стандартного» объема выборки, используемого в маркетинговых исследованиях. С чем же связан такой большой размер выборки?
Все дело в том, что клиенту были нужны оценки отдельно по каждому городу, а не просто «в целом по стране». Фактически мы работаем не с 1 выборкой, а с 33 отдельными выборками по каждому городу. Доля людей, заинтересованных в покупке квартиры в Санкт-Петербурге или Москве, была экспертно определена в рамках 5% от числа жителей опрашиваемых городов.
В зависимости от важности города для заказчика, руководитель проекта со стороны Агентства определил допустимую статистическую погрешность, в которую должны укладываться итоговые результаты. Для этого мы использовали специальный макрос в MS Excel, но эти расчеты можно также выполнить с помощью калькулятора выборки. В результате размер выборки варьировал от 500 до 1000 респондентов по каждому из городов исследования, что в сумме и дало заявленные 21 500 человек.
Резюме
Чтобы рассчитать выборку маркетингового исследования, используйте следующий алгоритм:
- Определите структуру целевой группы. Планируете ли вы анализировать отдельные подгруппы или достаточно будет анализа по выборке в целом?
- Определите желаемую точность данных. Например, если нужно оценить динамику рыночной доли за год, подставьте в специальный калькулятор примерное значение доли и «поиграйте» с разными объемами выборки.
- Найдите баланс между стоимостью сбора данных (прямо пропорциональна объему выборки) и требуемой точностью.


