Начало года выдалось весьма жарким, несмотря на морозную погоду, специфику сонного января и бушующий в российской экономике кризис. Проводя встречи с клиентами, мои коллеги почему-то именно сейчас неоднократно сталкивались с распространенным вопросом: “Наша целевая группа – примерно 50 / 100 / 500 тысяч человек. Как будет меняться размер выборки исходя из численности целевой группы?”.
Вопрос типичный, соответствует стереотипу о том, что чем больше численность целевой группы (на языке статистических терминов она называется “генеральной совокупностью”), тем больше должен быть размер выборки.
Между тем, этот стереотип не имеет ничего общего с реальностью – на самом деле, размер выборки в подавляющем большинстве случаев не зависит от численности генеральной совокупности и определяется другими факторами. Единственное исключение из этого правила – случаи, когда генеральная совокупность очень маленькая (например, 1-2 тысячи человек) и сопоставима по размеру с выборкой, но такие ситуации в реальной практике крайне редки.
Размер выборки зависит от двух факторов:
- Точности данных, которые необходимо получить на выходе (–> та самая “статистическая погрешность” данных);
- Количества и размера подгрупп, на которые нужно разбивать выборку при анализе – например, если проводится электоральное исследование и первоочередной интерес представляет ядро активных избирателей, которое – из общих соображений – редко превышает 20-25% населения в целом, нужно рассчитывать размер выборки таким образом, чтобы 1/4 от его размера позволяла проводить полноценный статистический анализ (т.е. была никак не меньше, чем 250-300 респондентов).
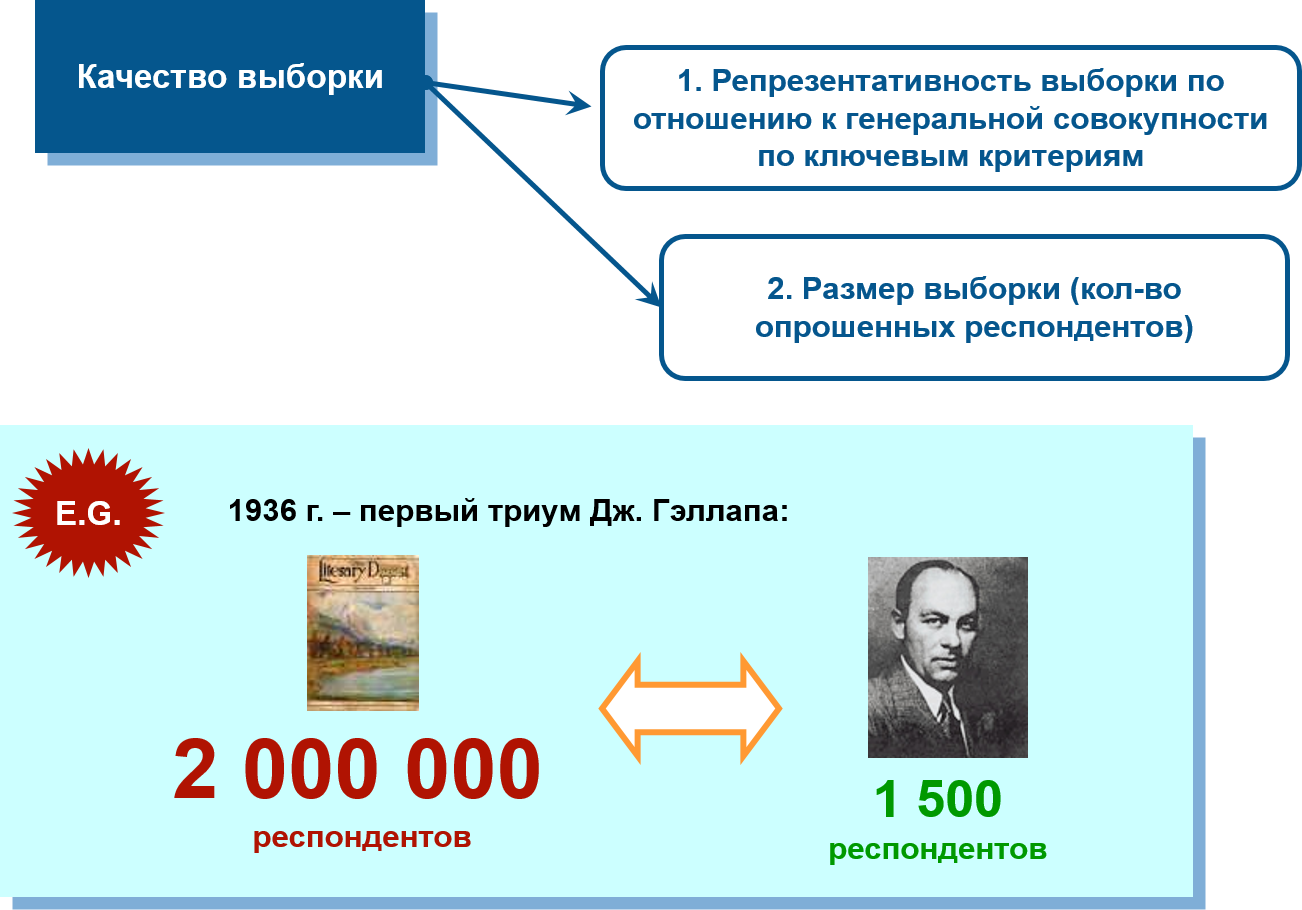
Качество выборки, опять же, вопреки расхожему мнению, определяется не столько ее размером, сколько репрезентативностью (т.е. соответствию) генеральной совокупности по ключевым переменным – чаще всего, в качестве таковых используют пол, возраст, образование, род занятий.
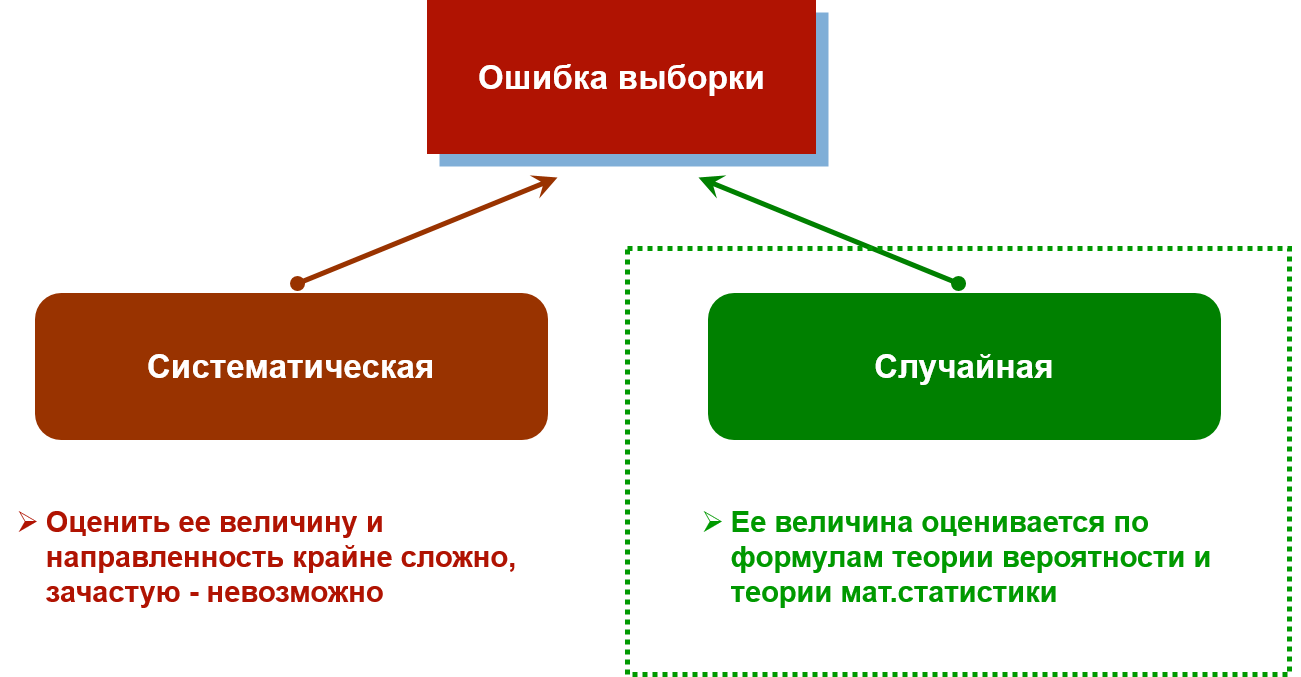
Выборочный метод предполагает наличие определенных расхождений между наблюдениями, полученными над выборкой, и распределением данного признака во всей генеральной совокупности. Величина этих расхождений и является “ошибкой выборки”, или статистической погрешностью.
Ошибка выборки может быть двух видов:
- Систематическая – связана с ошибками проектирования выборки, и оценить ее размер, направление и степень смещения крайне сложно. Например, если в качестве интервьюеров, общающихся с респондентами, будут выступать представители маргинальных социальных слоев, очевидно, что это повлияет на готовность участвовать в исследовании со стороны представителей более обеспеченных групп населения, а следовательно, приведет к крайне трудно оцениваемой систематической ошибке и искажению данных.
- Случайная – связана с действием законов статистики, ее размер легко рассчитывается по формулам теории вероятности и математической статистики. Случайная ошибка выборки зависит не только от объема выборки, но и от степени однородности данных. Чем однороднее данные (т.е. чем меньше разброс полученных значений, или дисперсия), тем меньше ошибка выборки.
Существует несложная формула расчета случайной ошибки выборки, однако для удобства рекомендуем пользоваться онлайн-калькуляторами, которые позволяют легко рассчитать как величину статистической погрешности на основе размера выборки и предполагаемой дисперсии, так и размер выборки, требуемый для получения оценки нужной степени точности.
http://surin.marketolog.biz/calculator.htm
В качестве параметра доверительной надежности (см. одно из полей в калькуляторе расчета) обычно используется значение в 95% – это означает, что в 95% случаев распределение признака в генеральной совокупности попадет в рассчитанный доверительный интервал (т.е. собственно значение признака в выборке плюс-минус размер статистической погрешности). Реже используется значение надежности в 97% или 99% – оно, соответственно, означает, что подобное попадание произойдет в 97% или 99% случаев, т.е. в данном случае надежность выборки повышается, но приводит к увеличению размера выборки.
Одна из самых сложных задач при определении размера выборки – поиск компромисса между требуемой точностью и стоимостью сбора данных. Поиск компромисса усложняется тем, что увеличение размера выборки в четыре раза приводит к увеличению точности лишь в два раза (т.е. квадратный корень от величины наращивания выборки).

